Contents

1.Introduction 2.Background 3.Experiment 4.Conclusion & Summary

본 글은 2017년에 발표된 Flow generative model의 일종인 Real NVP에 대한 논문 리뷰로 기본적인 Flow model에 대한 개념과 이전 논문인 NICE: Non-linear Independent Components Estimation 를 함께 보시는 것을 추천드립니다.

Flow model / NICE / Real NVP

Introduction

Why real NVP?

Real NVP의 저자들이 왜 이전 flow model인 NICE에서 발전을 시키고자 했는지를 이해하기 위해서는 우선 첫 논문인 NICE가 나왔던 2014년도의 생성 모델들에 대해서 이해해야합니다. 그 당시의 생성 모델들은 NADE (autoregressive model), VAE의 첫 논문 그리고 GAN의 첫 논문 등이 발표되던 시기로 생성 모델의 구조적 복잡성 보다는 모델의 새로운 아이디어 위주의 논문들이 발표 되던 시기였습니다. 그에 따라서 NICE 또한 addictive coupling layer라는 새롭지만 비교적 단순한 아이디어를 통해 jacobian과 inverse를 쉽게 구할 수 있는 형태를 구현함으로써 tractable하고 fast sampling 가능이 가능하며 representation learning까지 할 수 있는 초기의 flow model을 구현하였습니다.

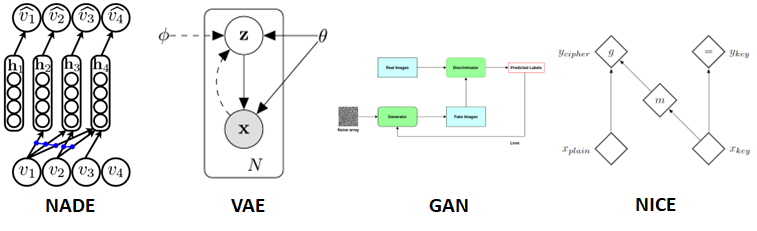
What is the problem?

아쉽게도 NICE는 간단한 분포로 mapping을 진행하는 transformation의 구조적 단순성으로 인해 두 가지 문제점이 발생했습니다. Transformation의 jacobian determinant이 항상 1이기 때문에 매 transformation 과정 중 data를 표현하는 subspace의 부피가 변하지 않는 Volume preserving transformation의 형태를 띌 뿐만 아니라 addictive coupling layer를 통해 업데이트 해주는 부분들이 미리 정해 놓은 mask를 통해 인위적으로 선별된 부분들만 업데이트가 된다. 이를 통해 매우 제한된 flexibility를 보여주게 되고 그로 인하 복잡한 데이터를 충분히 표현할 수 없었습니다.

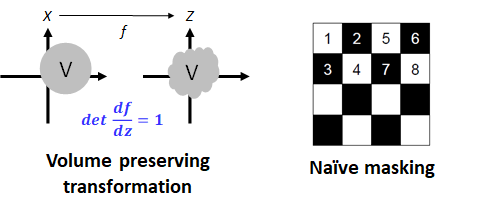
How the model is improved?

이런 문제점을 개선하기 위한 저자들의 Contribution은 다음과 같은 세 가지로 요약할 수 있습니다.

1) Affine coupling layer (non volume preserving transformation and complicated model) 2) Multi-scale architecture (efficient computation) 3) Channel-wise masking

저자들은 Affine coupling layer라는 새로운 transformation 구조를 통해 여전히 jacobian determinant와 inverse를 구하기 쉬운 구조를 유지하면서도 jacobian determinant의 값이 1이 아닌 다른 값이 가능하도록 변화를 줌으로써 Non-volume preserving transformation을 구현하였고, Multi-scale architecture라는 새로운 구조를 통해 더욱 깊은 Flow가 가능하도록 하였으며, 마지막으로 channel-wise masking을 통해 기존의 checker board masking보다 더욱 복잡한 형태로 Update를 할 데이터들을 선별하였습니다.

Background

1. Change of Variables

Flow model은 복잡한 분포의 반복적인 invertible transformation을 통해 간단한 분포(ex. 가우시안 분포)로 변환하는 것을 목표로 합니다. 이러한 반복적인 transformation은 데이터 분포의 흐름을 만들게 되며 이러한 성질로 Flow model이라는 이름 이 때, 데이터의 transformation을 통해 모델의 정확한 확률 분포를 계산할 필요가 있으며 이러한 연산의 기반이 Change of variable theorem이며 다음과 같은 계산 과정을 통해 진행됩니다.

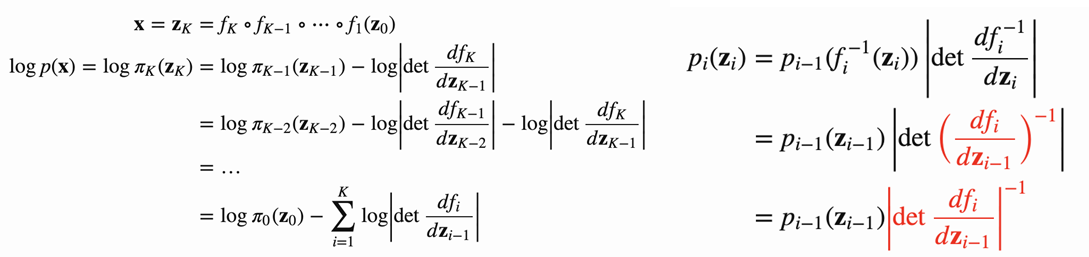
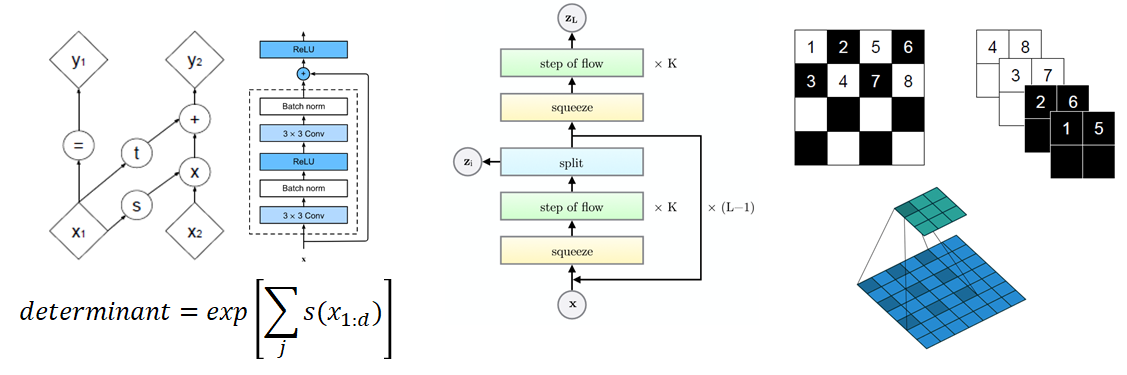
2. Affine Coupling Layers

Affine coupling layers는 기존 NICE의 additive coupling layer에서 더 복잡한 연산과정, 강력한 Neural networks model, Batch normalization을 적용하여 좀 더 복잡한 구조의 데이터를 잡아낼 수 있게끔 만든 것입니다.

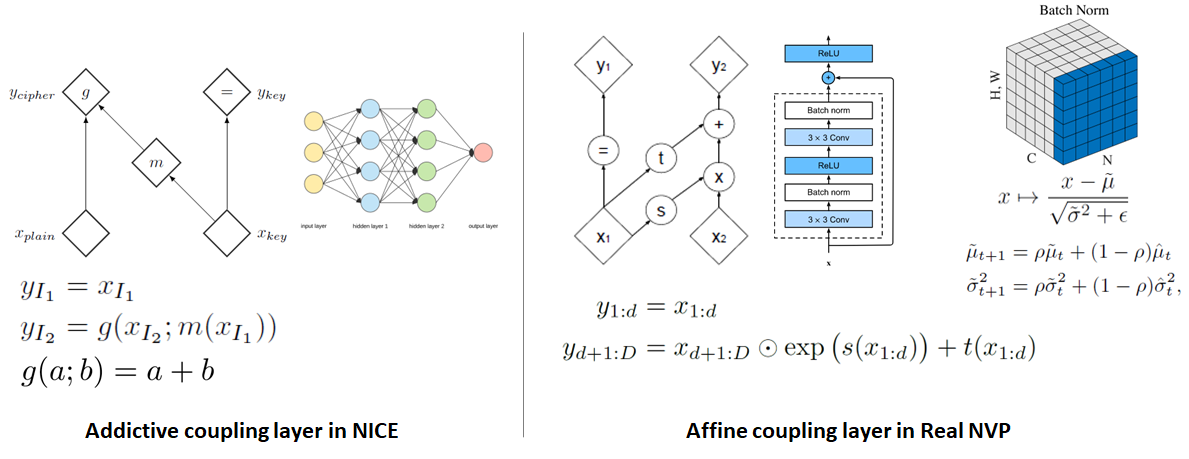
우선, 기존의 additive coupling layer가 단순한 덧셈 연산을 통해 transformation을 구현했다면, affine coupling layers는 덧셈 연산 외에도 지수 함수 부분을 추가로 넣어 주어 더욱 flexible한 연산이 가능해지도록 transformation 과정을 변경하였습니다. 뿐만 아니라 transformation에 사용되는 neural networks도 단순 multilayer perceptron에서 residual networks의 형태로 변경하여 복잡한 데이터도 충분히 처리할 수 있게끔 하였습니다. 마지막으로는 각 neural networks를 학습시킬 때 전체 레이어에 batch normalization을 적용하여 학습 자체도 더욱 정확하고 원활하게 일어날 수 있도록 하였습니다.

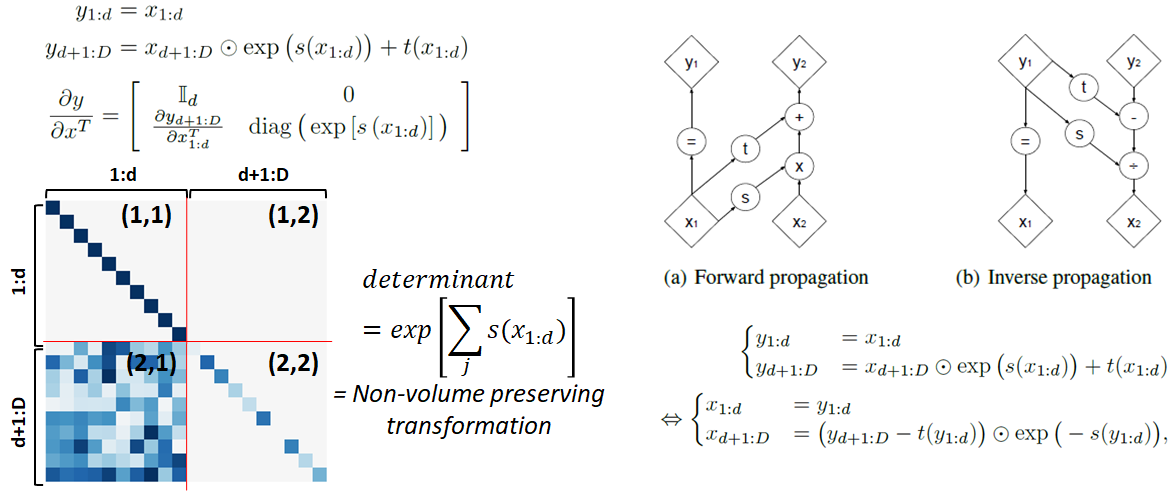
이렇게 변형된 Additive coupling layer는 여전히 jacobian determinant와 inverse를 구하기 쉬워야한다는 flow model의 조건을 만족하는 특징을 보입니다. Jacobian matrix는 여전이 NICE와 같이 triangular matrix의 형태를 띄고 있기 때문에 determinant가 jacobian matrix의 대각 성분들로만 계산할 수 있으며 그 과정에서 1이 아닌 값을 보여주기 때문에 Non-volume preserving transformation이 가능해집니다. Inverse 또한 기존 transformation 식의 간단한 이항을 통해 손 쉽게 계산될 수 있습니다. 이 모든 과정에서 neural networks의 jacobian이 계산될 필요가 없기 때문에 affine coupling layer는 여전히 jacobian determinant와 inverse를 구하기 쉽다는 성질이 유지됩니다.

3. Masked Convolution

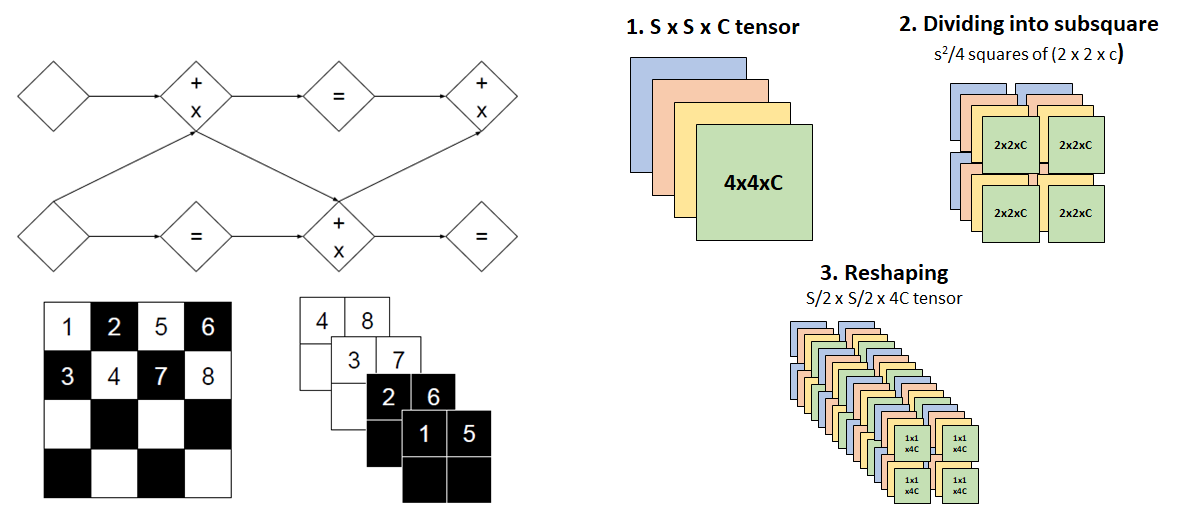
NICE의 단순성을 만들었던 나머지 요인인 checker board masking은 channel-wise masking을 통해 개선되었습니다. NICE와 마찬가지로 Real NVP에서는 affine coupling layer를 업데이트되지 않는 부분들(Fig.6 마스크의 검은 부분)이 존재하기 때문에 업데이트될 부분들을 alternating하게 affine coupling layer에 넣어주어 모든 데이터들이 변할 수 있게 만들어 줍니다. 이 과정에서 업데이트되는 부분을 선별할 때 NICE와 같이 checker board 형태로 선별할 뿐만 아니라 channel-wise한 방식으로 선별하여 데이터들이 좀 더 다양하게 섞일 수 있도록 만들어 줍니다. 또한, channel-wise masking가 항상 같이 업데이트 되던 채널끼리만 묶이게 되는 상황을 방지하기 위해 squeezing이라는 연산을 추가적으로 진행하는데, squeezing은 기존의 SSC의 데이터를 22c의 여러 subsquare로 분산한 뒤 subsquare-wise한 방식으로 각 subsquare들을 S/2S/24C의 형태로 reshape을 해주는 연산입니다. 이러한 연산을 통해 각 채널은 고정된 상태로 alternating한 방식으로 업데이트되는 것이 아니라 매 squeezing 과정에서 서로 섞이는 효과를 만들어내고 이를 통해 좀 더 복잡한 형태의 업데이트가 가능해집니다.

4. Multi-Scale Architecture

Affine coupling layer는 jacobian determinant와 inverse를 구하기 쉽게 만들기 위해 제약 조건이 강하게 걸린 transformation이라고 말할 수 있습니다. 따라서 매 transformation을 통해 바꿀 수 있는 데이터의 분포는 매우 제한적이며 좀 더 복잡한 데이터를 처리하기 위해서는 필연적으로 매우 깊은 구조로 coupling layer를 쌓을 수 밖에 없습니다. Multi-scale architecture는 이 깊은 구조를 효과적으로 구현하기 위해 제안된 구조입니다.

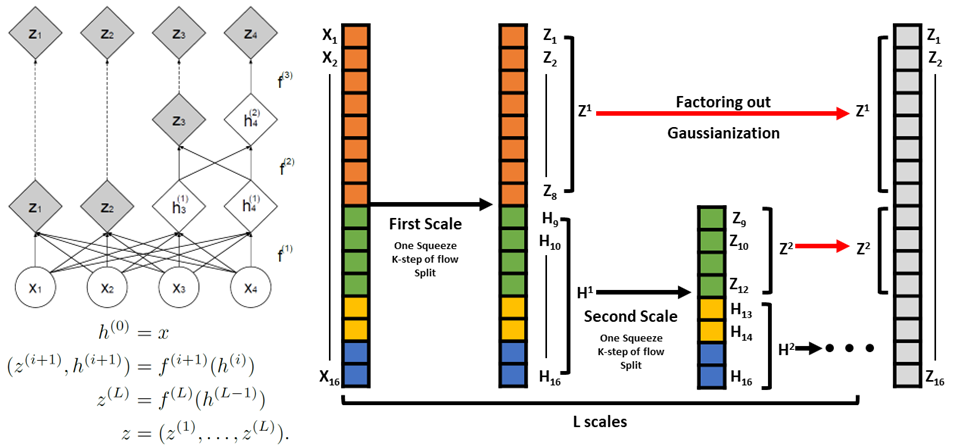
저자들이 제안한 방법은 scale 구조와 매 scale 시 반복되는 factoring out입니다. Scale은 저자들이 정해 놓은 일련의 sequential한 transformation 과정으로 한 scale 내에서 checker board masking을 활용한 3번의 transformation을 진행한 후 한번의 squeezing 연산을 통해 channel을 섞은 다음 channel-wise masking을 통해 3번의 transformation을 진행하게 됩니다. 이 때, 저자들은 scale을 한번 거친 후 사용된 변수들 중 절반을 강제로 가우시안 분포를 따르게 만들고 가우시안화된 변수들은 다음 스케일에서 사용하지 않은 factoring out 방법을 적용합니다. 이로 인해 매 scale이 지날 때 마다 변수는 절반으로 줄어들게 되며 이를 통해 전체적으로 사용되는 모델의 개수도 줄어들게 되어 computation의 부담을 줄일 수 있게 됩니다. 뿐만 아니라, factoring out을 통하여 low level feature와 high level feature를 고르게 학습할 수 있게 되므로 전체적인 모델 성능도 개선될 수 있게 됩니다.

저자들이 제안한 factoring out의 효과는 다음과 같은 실험을 통해 검증되었습니다. 저자들은 기존의 이미지를 high level feature는 유지하며 low level feature들만을 변화시키며 resampling을 진행하였습니다. 이를 통해 아래의 이미지들과 같은 resampling 결과를 었었습니다(왼쪽부터 100%, 50%, 25%, 12.5%, 6.25%의 high level feature들을 고정시키며 나머지 low level feature들을 변화시킨 것). 이를 통해 저자들은 high level feature들은 이미지 전반에 대한 맥락적인 정보들을 담고 있으며 low level feature들은 이미지의 그래픽적인 디테일에 대한 정보들을 담고 있음을 보였으며 factoring out 방식을 통해 high level과 low level의 feature들을 고르게 학습할 수 있음을 확인하였습니다.

Experiment

우선 수치적으로 비교한 결과입니다. Real NVP의 경우 당시 매우 우수한 성능을 보인 PixelRNN에 비하면 다소 아쉬운 성능을 보이지만, 다른 모델들과 비교해 보았을 경우에는 충분히 경쟁력 있는 성능을 보이는 것이 확인되었습니다.

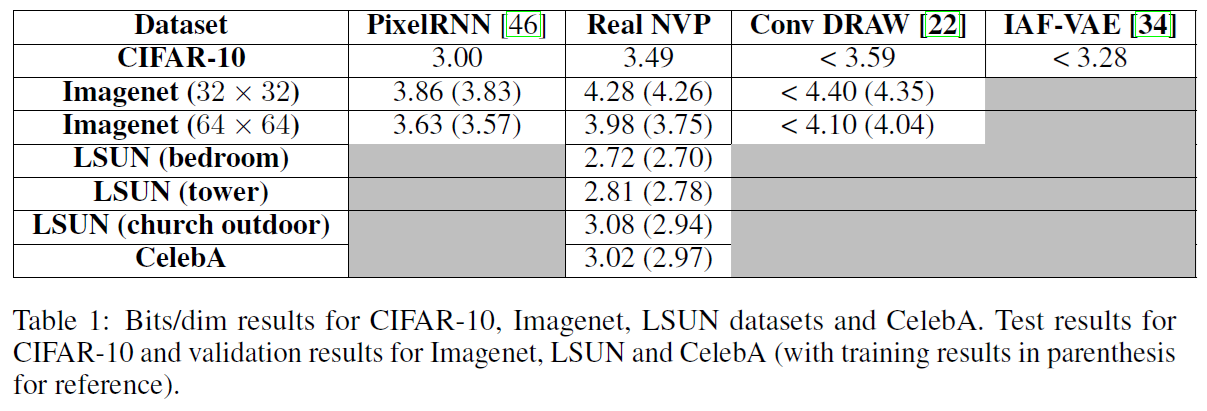
또한 Autoregressive model에 비해 여전히 샘플링 속도도 충분히 빠른 것이 확인되었으며 샘플링된 이미지들의 품질 또한 매우 우수하게 나타났습니다. 특히나 이전 논문들과는 다르게 Low level feature의 구현을 기반으로 이미지의 디테일이 살아난 sharp한 이미지의 생성이 가능해졌습니다.

마지막으로 저자들은 representation learning을 통해 semantically meaningful representation을 학습했는지 살펴봤습니다. 저자들은 latent space 내에서 sample간의 interpolation이 이미지가 continuous하게 변화하는 결과로 이어지는 것을 통해 latent space가 consistent한 학습을 하였다고 주장합니다.

Conclusion & Summary

정리해 보자면, 저자들은 다음과 같은 방법들을 통해 좀 개선된 모델을 구축하여 좀 더 복잡한 구조의 데이터도 처리할 수 있는 Real NVP를 제안하였습니다.

1) Affine coupling layer (non volume preserving transformation and complicated model) 2) Multi-scale architecture (efficient computation) 3) Channel-wise masking

이러한 모델은 다양한 변화에도 여전히 tractable하고 fast sampling이 가능하며 데이터에 대한 representation learning까지 가능한 성질을 잘 나타내고 있는 flow model이라 할 수 있습니다. 하지만 이러한 개선점에도 다음과 같은 문제점들이 여전히 존재하고 있습니다.

1) Permutation of update variables is still fixed manner 2) Non volume preserving might cause extremely small determinant, almost 0 (not trainable) 3) Affine transformation is very limited transformation

Masking을 통한 업데이트는 여전히 인위적으로 이루어지고 있기 때문에 더 복잡하게 만들 필요가 있으며 transformation의 Non volume preserving이라는 성질로 인해 jacobian determinant가 0에 가까워지는 현상이 발생에 학습이 불가능해지는 경우가 발생할 수 있고 affine coupling layer는 매우 제한적인 변환이기 때문에 복잡한 데이터를 충분히 표현하기에는 여전히 제한적인 변환입니다 .

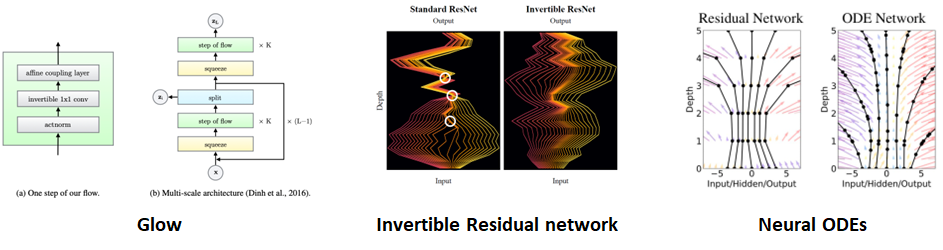
다행히 후속 연구에서 제시된 문제점을 해결하기 위한 시도들이 존재합니다. Masking을 통한 인위적인 업데이트에서 발생하는 문제점은 “Glow: Generative Flow with Invertible 1x1 Convolutions”라는 논문에서 1x1 convolution을 통해 학습 가능한 masking을 구현하여 업데이트를 해줄 부분을 학습을 통해 배워나가는 접근법이 존재합니다.

또 다른 후속 연구로써 Scale의 factoring out이 residual networks의 skip connection과 유사하다는 아이디어에서 출발하여 residual networks 자체를 invertible하게 구현한 “Invertible Residual Networks” 의 연구도 존재하며, 이 연구에서 발전하여 한 layer에서 다음 layer로 넘어가는 연산이 discrete하게 구현되지 않고 activation function 부분을 ODEs로써 구현하여 다음 layer로 넘어가는 연산이 continuous하게 일어나게 만들어 주는 “Neural Ordinary Differential Equations”이라는 연구도 존재합니다.